Research

準結晶の相関物性 | Correlated electrons in quasicrystals

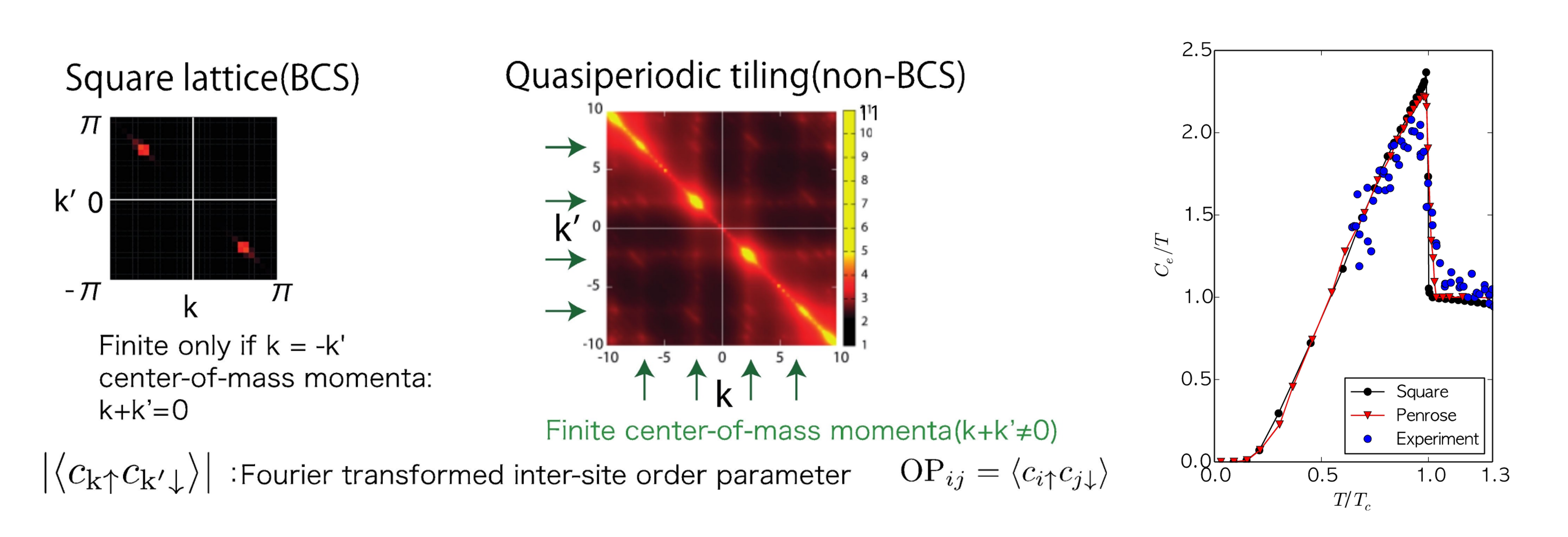
準結晶の発見以来、準周期性は大きな関心を集めてきました。主な関心の一つは、並進対称性を持たない長距離秩序の存在の可能性である。2011年に最初の強相関準結晶(Au-Al-Yb)が合成され、周期構造を持つ近似結晶では現れない量子臨界性が発見されました。また、2018年には準結晶(Al-Mg-Zn)で初めてバルク超伝導が観測されました。しかし、準周期系は並進対称性がないため、相関効果を理論的に扱うことは困難な問題でした。 我々は、力学的平均場法を拡張した実空間力学的平均場法をこの系に適用することを提案しました。特に、当時まだ発見されていなかった超伝導準結晶の理論的研究を進め、 有限の重心運動量を持つクーパー対の出現を発見しました。さらに、弱結合準周期超伝導体の比熱のがBCS理論跳びの値より15%小さいことを明らかにし、実験結果の比熱の跳びの減少を説明しました。

Quasiperiodicity have attracted considerable interest since the discovery of quasicrystals. One of the major interests is in a possible existence of a long-range order without translational symmetry. The first strongly correlated quasicrystal (Au-Al-Yb) has been synthesized in 2011. The quantum criticality which does not appear in the approximant with the periodic structure has been found. The first bulk superconductivity in quasicrystal (Al-Mg-Zn) has also observed in 2018. However, it is difficult to treat the quasiperiodic system and the correlation effect theoretically since there is no translational symmetry. We proposed applying real-space dynamical mean-field method, an extension of the dynamical mean-field method to this system. Especially, we pursued theoretical investigation on superconducting quasicrystals, which had not yet been discovered at the time and found, the appearance of cooper pairs with center of mass momentum. Furthermore, we clarifiedthe specific heat jump in weak-coupling quasiperiodic superconductors is 15% smaller than the value in BCS theory, which explains the reduction in the specific heat jump in the experimental results.

量子アルゴリズム開発 | Quantum algorithms

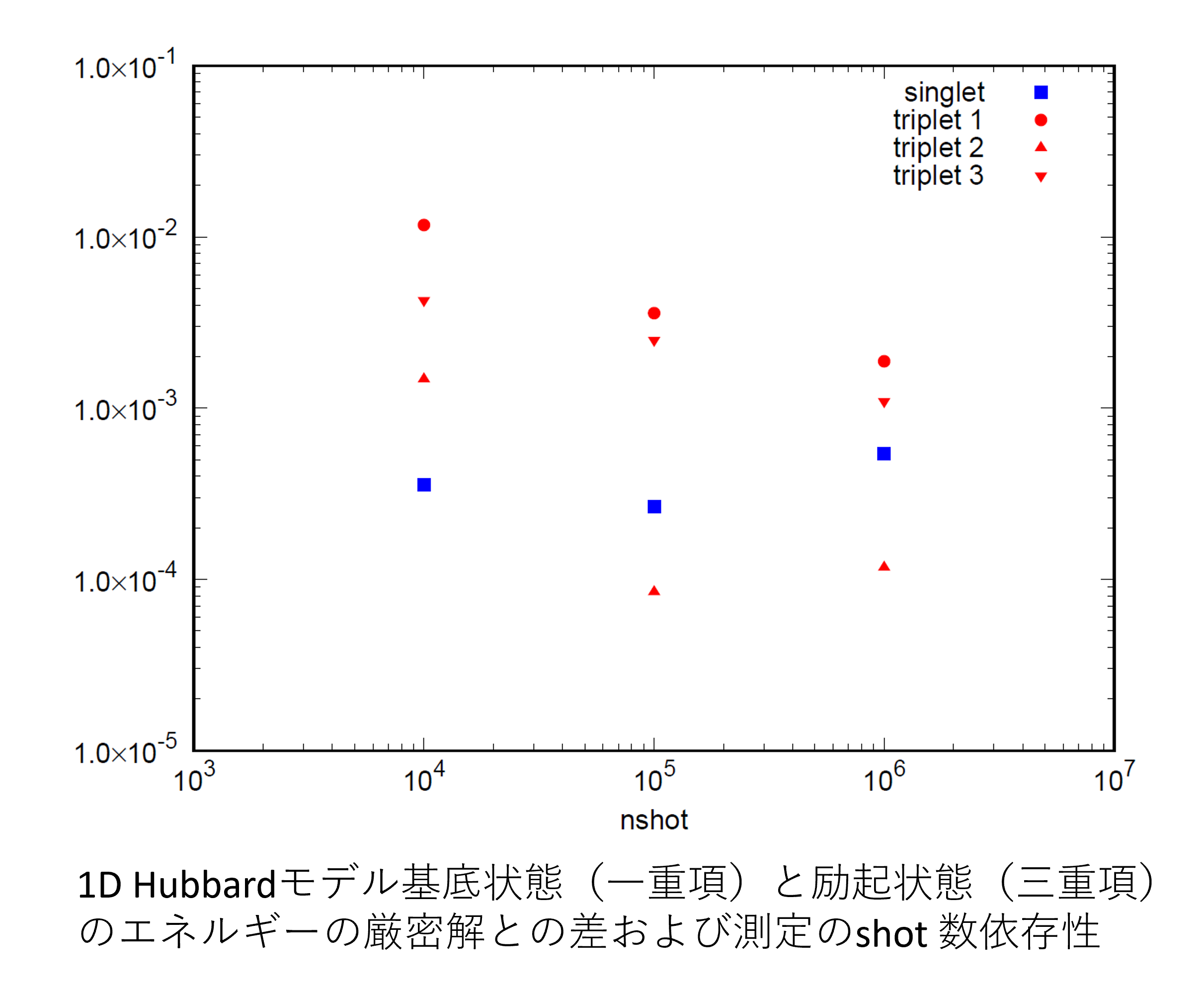
量子アルゴリズムは、量子コンピュータを用いて問題解くためアルゴリズムのことで、本研究室では、特に物性物理学の文脈において、これらのアルゴリズムを強化することに焦点を当てています。例えば、量子多体系において重要なステップである縮小密度行列（RDM）の評価を改善に取り組んでいます。フェルミオンシャドウ法を用いることで、高次の縮約密度行列を効率的に再構成し、量子部分空間展開法の大きなボトルネックを克服する方法を提案しています。このアプローチは、強相関電子系の量子ソルバーを発展させる可能性を秘めている。 さらに、物性物理学の手法を量子化学に応用し、効率的に量子コンピューターでシミュレートするための研究も行っています。これらの研究を通して、複雑な物理系のより効率的な量子シミュレーションに貢献しています。

Quantum algorithms provide powerful tools for solving problems in quantum computers. We focus on enhancing these algorithms, particularly in the context of condensed matter physics. One key aspect is improving the evaluation of reduced density matrices (RDMs), a crucial step in quantum many-body systems. By using the fermionic shadow method, We aim to efficiently reconstruct higher-order contraction density matrices, overcoming a significant bottleneck in the quantum subspace expansion method. This approach holds potential for advancing quantum solvers for strongly correlated electron systems. Additionally, we are exploring the application of condensed matter physics techniques to quantum chemistry. These advances contribute to more efficient quantum simulations of complex physical systems.